
Liquids and Glasses
Research in my group addresses fundamental questions in the physical chemistry of liquids, liquid mixtures, and glasses, and applies this knowledge to the solution of problems of interest in modern chemical engineering. Examples of recent and ongoing activities include theoretical and computational studies of the dynamics and thermodynamics of glass-forming liquids; theoretical and computational studies of supercooled, and glassy water, and of water confined by surfaces with tunable patterns of hydrophobicity and hydrophilicity; the development of theories of hydrophobic hydration; the quantification of disorder in materials; the development of molecular theories of metastability and nucleation; and the derivation of improved algorithms for the simulation of glasses and biomolecules. This work finds applications in a wide range of areas and practical problems, such as the self-assembly of biological molecules, microfluidic technologies, the engineering of protein stability, and climate modeling.
Water and Aqueous Solutions
(11, 16, 32, 42, 52, 59, 60, 62, 66, 75, 76, 87, 93, 102, 103, 109, 115, 116, 121, 128, 129, 137, 138, 141, 144, 146, 152, 153, 155)
The peculiar properties of water include expansion upon cooling, contraction upon melting, increased fluidity upon compression, anomalously large heat capacity and dielectric constant,
unusually high melting and boiling temperatures, and compressibility minima. Water’s anomalies become more pronounced when it is cooled below the freezing point without crystallizing
(supercooled). For example, its isothermal compressibility, isobaric heat capacity, and the magnitude of the thermal expansion coefficient increase sharply upon cooling, and
 power-law extrapolations of many thermophysical properties appear to diverge close to 45oC. Because supercooled water’s anomalies are but low-temperature exacerbations of behavior
that is already evident in the normal range of stability, understanding their microscopic origin and thermodynamic consequences is essential to a still elusive physical picture of
this most important of substances. Our goal is to understand the molecular basis and thermodynamic consequences of these anomalies. Of particular interest is the possibility that two
power-law extrapolations of many thermophysical properties appear to diverge close to 45oC. Because supercooled water’s anomalies are but low-temperature exacerbations of behavior
that is already evident in the normal range of stability, understanding their microscopic origin and thermodynamic consequences is essential to a still elusive physical picture of
this most important of substances. Our goal is to understand the molecular basis and thermodynamic consequences of these anomalies. Of particular interest is the possibility that two
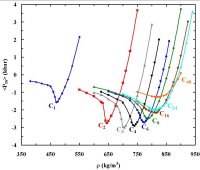
 distinct forms of supercooled water may coexist. This conjecture follows from experimental observations suggesting the existence of two forms of glassy water, separated by an a
apparently first-order transition. We have developed microscopic models that reproduce all the thermodynamically consistent scenarios that can explain experimental observations
(59,62,66,76). A model that incorporates hydrogen bond directionality results in an equation of state that reproduces, with remarkable accuracy, the compressibility, thermal expansion,
distinct forms of supercooled water may coexist. This conjecture follows from experimental observations suggesting the existence of two forms of glassy water, separated by an a
apparently first-order transition. We have developed microscopic models that reproduce all the thermodynamically consistent scenarios that can explain experimental observations
(59,62,66,76). A model that incorporates hydrogen bond directionality results in an equation of state that reproduces, with remarkable accuracy, the compressibility, thermal expansion,
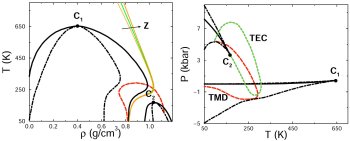 and heat capacity anomalies over broad ranges of temperature and pressure, in addition to predicting all of the global phase behaviors that are consistent with the experimental
observations (87). The model also yields useful insights into the thermodynamics of confined water, with possible implications for the hydration of non-polar solutes and the
stabilization of biologically significant structures of proteins in solution (103,109). Recently we used this model to study the phase behavior of binary mixtures in which one
and heat capacity anomalies over broad ranges of temperature and pressure, in addition to predicting all of the global phase behaviors that are consistent with the experimental
observations (87). The model also yields useful insights into the thermodynamics of confined water, with possible implications for the hydration of non-polar solutes and the
stabilization of biologically significant structures of proteins in solution (103,109). Recently we used this model to study the phase behavior of binary mixtures in which one
 component can have more than one critical point (153). Such hitherto unexplored type of mixture phase diagrams are not only inherently interesting,
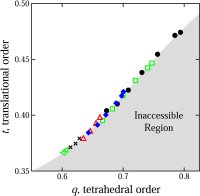
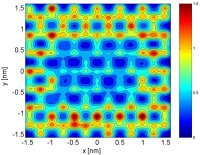
but may hold clues to pure water's metastable phase behavior. We developed a computational method for quantifying structural order in water and showed how liquid water’s unusual
propensity for order gives rise to its anomalous transport and thermodynamic properties (102); the method has also been applied to the study of structural order in water glasses
component can have more than one critical point (153). Such hitherto unexplored type of mixture phase diagrams are not only inherently interesting,
but may hold clues to pure water's metastable phase behavior. We developed a computational method for quantifying structural order in water and showed how liquid water’s unusual
propensity for order gives rise to its anomalous transport and thermodynamic properties (102); the method has also been applied to the study of structural order in water glasses
 (144). In ongoing work, we are investigating the structure, dynamics, and thermodynamics of water confined by surfaces with engineered patterns of hydrophobicity and hydrophilicity
(152). This project has implications ranging from protein folding to the design of super-hydrophobic surfaces. We are also investigating the structural, transport, and thermodynamic
properties of modified water models in which either the geometry or the relative importance of electrostatic and dispersion forces are systematically perturbed about those
corresponding to water (141).
(144). In ongoing work, we are investigating the structure, dynamics, and thermodynamics of water confined by surfaces with engineered patterns of hydrophobicity and hydrophilicity
(152). This project has implications ranging from protein folding to the design of super-hydrophobic surfaces. We are also investigating the structural, transport, and thermodynamic
properties of modified water models in which either the geometry or the relative importance of electrostatic and dispersion forces are systematically perturbed about those
corresponding to water (141).
Supercooled Liquids and Glasses
(46, 54, 64, 69, 70, 74, 77, 78, 80, 85, 91, 94, 95, 96, 97, 98, 105, 106, 107, 108, 110, 113, 114, 119, 120, 123, 124, 125, 130, 131, 133, 134, 140, 147, 148)

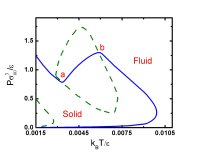
There are important gaps in our understanding of the thermophysical properties of supercooled liquids (105,book chapter 11). The viscosity of some liquids exhibits Arrhenius
temperature dependence, while others deviate markedly from this behavior. The coupling between diffusion coeffcient and viscosity, embodied by the Stokes-Einstein equation, as well
 as that existing between rotational and translational relaxation, break down for many supercooled liquids. A microscopically-based, fundamental understanding of the dynamics of
supercooled liquids is lacking. Because the viscosity of liquids increases by many orders of magnitude upon cooling in the vicinity if the glass transition, accurate knowledge of
as that existing between rotational and translational relaxation, break down for many supercooled liquids. A microscopically-based, fundamental understanding of the dynamics of
supercooled liquids is lacking. Because the viscosity of liquids increases by many orders of magnitude upon cooling in the vicinity if the glass transition, accurate knowledge of
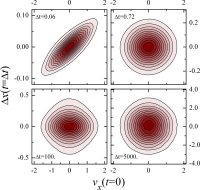 this temperature dependence is desirable in the processing of melts. An appealing approach is to consider the influence of a system’s “energy landscape” on the relaxation processes
it displays. The dynamics of the system is viewed as the motion of the state point (described by the coordinates of all particles in the 3N-dimensional configuration space, where
this temperature dependence is desirable in the processing of melts. An appealing approach is to consider the influence of a system’s “energy landscape” on the relaxation processes
it displays. The dynamics of the system is viewed as the motion of the state point (described by the coordinates of all particles in the 3N-dimensional configuration space, where
 N is the number of particles). The potential energy of the system, a function of particle coordinates, defines a complicated 3N-dimensional surface or “landscape”. The configuration
space can be partitioned into basins, such that a local minimization of potential energy maps any point in a basin onto the same minimum. The properties of the system at a given
N is the number of particles). The potential energy of the system, a function of particle coordinates, defines a complicated 3N-dimensional surface or “landscape”. The configuration
space can be partitioned into basins, such that a local minimization of potential energy maps any point in a basin onto the same minimum. The properties of the system at a given
 temperature are dictated by the basins that it samples, and by their mutual accessibility. We have used this energy landscape approach to demonstrate, via computer
simulations, that the onset of non-exponential relaxation and of non-Arrhenius dependence of the structural relaxation time correspond to a well-defined temperature below which the
temperature are dictated by the basins that it samples, and by their mutual accessibility. We have used this energy landscape approach to demonstrate, via computer
simulations, that the onset of non-exponential relaxation and of non-Arrhenius dependence of the structural relaxation time correspond to a well-defined temperature below which the
 the depth of the potential energy minima explored by the liquid decreases with temperature, and above which it does not (74, 94). The energy landscape also provides valuable insight
into the mechanical stability of liquids (70, 91), aging phenomena in glasses (95), and the mechanical properties of amorphous materials (106,114). Thermodynamic thinking about the
the depth of the potential energy minima explored by the liquid decreases with temperature, and above which it does not (74, 94). The energy landscape also provides valuable insight
into the mechanical stability of liquids (70, 91), aging phenomena in glasses (95), and the mechanical properties of amorphous materials (106,114). Thermodynamic thinking about the
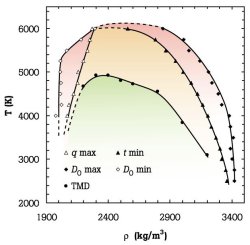 glassy state of matter dates back to the pioneering work of Simon and Kauzmann, whose profound implications are a subject of continued interest (108,110,123,124). Recent work has
addressed the thermodynamics and statistical mechanics of inverse melting (liquids that freeze when heated) (123,124), the derivation of equations of state based on energy landscape
statistics (120,130,131,133), the extension of the thermodynamic formalism to encompass saddles in the energy landscape (131) and the theoretical (142) and computational (147,148)
investigation of alternative expressions for the diffusion coefficient and their application to diffusive motion and dynamic heterogeneity in supercooled liquids.
glassy state of matter dates back to the pioneering work of Simon and Kauzmann, whose profound implications are a subject of continued interest (108,110,123,124). Recent work has
addressed the thermodynamics and statistical mechanics of inverse melting (liquids that freeze when heated) (123,124), the derivation of equations of state based on energy landscape
statistics (120,130,131,133), the extension of the thermodynamic formalism to encompass saddles in the energy landscape (131) and the theoretical (142) and computational (147,148)
investigation of alternative expressions for the diffusion coefficient and their application to diffusive motion and dynamic heterogeneity in supercooled liquids.
Theory of Nucleation
(27, 72, 88, 89, 104, 118)
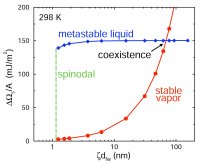
First-order phase transitions occur by two fundamental mechanisms: nucleation and growth, and spinodal decomposition (Book chapters 10). The former occurs when the starting condition is metastable, the latter, when the starting condition is unstable. Nucleation is an activated process: a free energy barrier (critical nucleus) must be overcome (formed) before the more stable phase appears. In contrast, spinodal decomposition is spontaneous. Rain, acid rain, air pollution, vapor-phase synthesis of materials, and industrial crystallization are but a few of the important natural and technical phenomena and processes in which nucleation plays a key role. Yet, despite nucleation's ubiquity and importance, the accurate prediction of nucleation rates is only possible for the simplest of physical systems. We are interested in the fundamental theory of nucleation, and have recently derived rigorous expressions for the free energy barriers to the formation of microscopic embryos of a new phase within a uniform metastable mother phase (72, 89). These expressions extend and generalize the classic work of Gibbs to the case where the embryo is not in unstable equilibrium with the mother phase. We are currently using molecular simulations (88), density functional theory (104), and kinetic theory (118) to study bubble nucleation in superheated liquids.
Statistical Geometry
(69, 70, 77, 80, 86, 96, 97, 98, 100, 101, 102, 113, 116, 119, 144, 155)
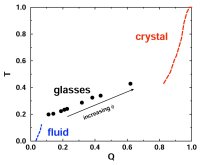
The structure of dense liquids is governed by repulsive interactions, while attractions can, for most practical purposes, be thought of as providing a uniform background cohesive
potential. Hard spheres are therefore the natural reference system in descriptions of the liquid state. Hard spheres are also the simplest non-trivial system to exhibit a first-order
 phase transition (freezing). Because of this, hard spheres continue to play a central role in the theory of liquids. Geometry and thermodynamics are indistinguishable in hard sphere
systems. In other words, one can calculate the equation of state and chemical potential of a hard sphere system from knowledge of such quantities as the mean cavity volume and the
phase transition (freezing). Because of this, hard spheres continue to play a central role in the theory of liquids. Geometry and thermodynamics are indistinguishable in hard sphere
systems. In other words, one can calculate the equation of state and chemical potential of a hard sphere system from knowledge of such quantities as the mean cavity volume and the
 mean interface area between cavities and spheres (100,101). Recently we have derived an algorithm for the exact calulation of conectivity, void volume, and surface area in mono- and
polydisperse sphere packings (69). This information is important in flow through porous media, protein solvation, add the characterization of random media, in addition to the
mean interface area between cavities and spheres (100,101). Recently we have derived an algorithm for the exact calulation of conectivity, void volume, and surface area in mono- and
polydisperse sphere packings (69). This information is important in flow through porous media, protein solvation, add the characterization of random media, in addition to the
 thermodynamics of hard spheres. We are applying this algorithm the study of supercooled hard spheres and hard disks (80), bubble nucleation (70,88), and the mechanical strength of
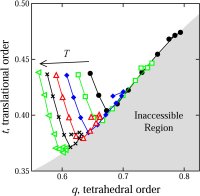
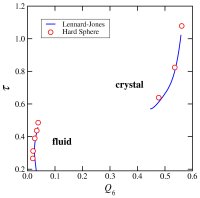
glasses (70,91,106,114). We developed a new method for the quantification of structural order (or its complement, disorder) in materials, which involves mapping equilibrium states
(or configurations) onto a space whose coordinates are order parameters for the system of interest. The resulting representation, an order phase diagram or order map, has been used
to quantify structure order in hard spheres (96,97), the Lennard-Jones system (119), liquid and glassy water (102,144), and families of fluids that span the range of behavior from
hard spheres to water (155).
thermodynamics of hard spheres. We are applying this algorithm the study of supercooled hard spheres and hard disks (80), bubble nucleation (70,88), and the mechanical strength of
glasses (70,91,106,114). We developed a new method for the quantification of structural order (or its complement, disorder) in materials, which involves mapping equilibrium states
(or configurations) onto a space whose coordinates are order parameters for the system of interest. The resulting representation, an order phase diagram or order map, has been used
to quantify structure order in hard spheres (96,97), the Lennard-Jones system (119), liquid and glassy water (102,144), and families of fluids that span the range of behavior from
hard spheres to water (155).
(*) Numbers in parenthesis refer to articles in the chronological bibliography.
